二元堆積 (Binary Heap)、最小堆積 (Min Heap) 與最大堆積 (Max Heap)

March 07, 2022

Binary Heap (二元堆積) 是一種常見的資料結構，適合需要取最大最小值的場合，也適合用來解決 top-k 問題，同時也常被用來實作 priortity queue (優先權佇列)。在 Dijkstra 演算法中，堆積也扮演了重要的角色。Binary Heap 取出最大/最小值的時間複雜度為 O(logN)，而插入元素需要 O(logN) 的時間複雜度。

Binary Heap 是什麼

Binary heap 有兩個特點：

Binary heap 是一個完全二元樹 (complete binary tree)，完全樹的意思是除了最後一層外每一層都填滿，最後一層必須由左至右填入。
Max heap 的每個結點的值，大於其左節點的值和右節點的值，根節點是整棵樹最大的節點；Min heap 每個結點的值，小於其左節點的值和右節點的值，根節點是整棵樹最小的節點。

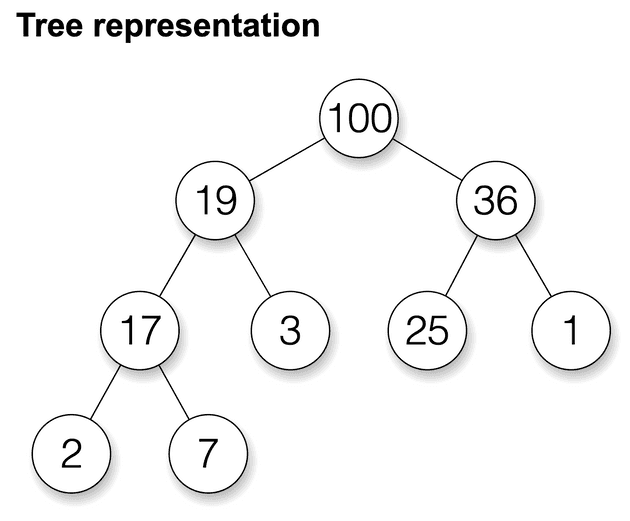
圖片來源：Wikipedia

上面是一個 max heap tree 的例子：根節點是 100，也是整棵樹的最大值，其左節點和右節點分別為 19 及 36，小於根節點的 100。樹中每個節點的左節點和右節點均小於父節點。

整棵樹除了最後一層以外均填滿，最後一層的節點由左至右依序填入，是一顆完全二元樹 (complete binary tree)。

Binary Heap 有兩個主要的操作： insert() 和 extract_max()。

insert()

當我們插入元素到 binary heap 時，有以下幾個步驟要執行：

先將欲插入的元素放入 binary heap 的最後一個位置
比較此元素和父節點的值，有必要的時候交換。以 max heap 為例，父節點必須比子節點還大，因此如果子節點比父節點還大，就將其與父節點交換位置。
繼續對父節點重複此比較的過程，直到不能再向上移動為止。

這個操作又稱為 “swim”。

下列影片示範插入一個數字到 max heap 的過程：

insert() 的時間複雜度是 O(logN)，因為需要跟分支上的元素作比較，分支的高度是 O(logN)。

extract_max()

當我們要取出最大值時，只要把樹的根節點取出即可。問題是要如何更新整棵樹的結構，使得刪除完之後還是一棵 binary heap tree？

刪除的步驟如下：

取出最大的元素，也就是根節點，並且和樹的最後一個節點交換。
比較根節點和左右子節點，如果子節點較大則和根節點交換。如果左右子節點都比較大，則跟較大者交換，因為要維持 max heap 父節點大於子節點的結構。
繼續對子節點重複與子節點比較的過程，直到不能再向下移動為止。

這個操作又稱為 “sink”。

下列影片示範將最大值從 max heap 取出的過程：

此操作的時間複雜度為 O(logN)。

使用 array 實作 heap

概念上 binary heap / max heap / min heap 是一個樹狀結構，但實務上我們可以不用 tree 而是用 array 來實作。這是怎麼做到的呢？

用 array 來實作 complete binary tree 有幾個重點：

index = 0 是根節點
對 index = n 的節點，其左子節點 index = 2 * n + 1，右子節點 index = 2 * n + 2。
對 index = n 的節點，其父節點 index = (n - 1) // 2，其中 // 表示整數除法。

按照這樣的存法，就可以把一棵完全二元樹連續不間斷地放進一個 array 裡面。

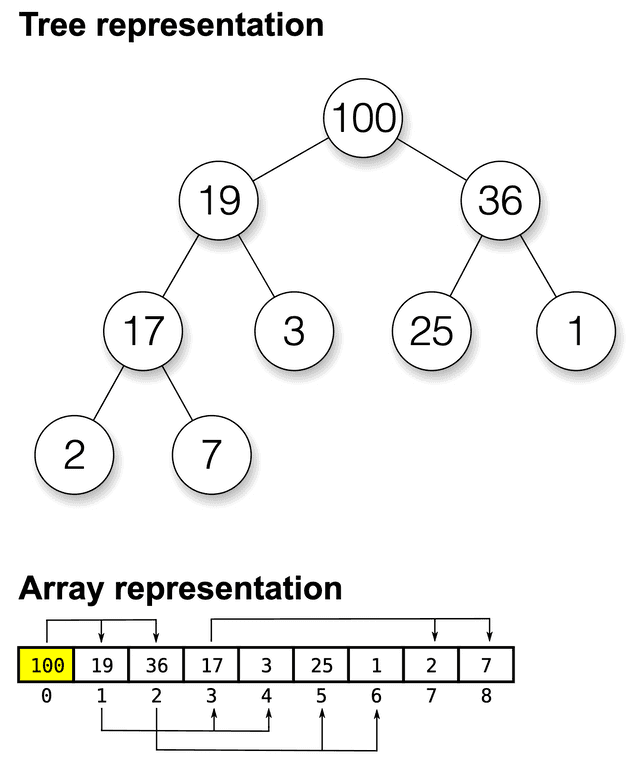
如下圖，一棵 binary heap tree 可以用以下 array 的結構儲存：

圖片來源：Wikipedia

舉例來說，index = 3 的節點，其左子節點 index = 2 * 3 + 1 = 7, 右子節點 index = 2 * 3 + 2 = 8，其父節點為 index = (3 - 1) // 2 = 1。

用 Python 實作 Heap

下列 python 程式碼實作了 max heap 的 insert() 和 extract_max() 兩種操作。

注意以下兩個重點：

insert() 時，我們將元素插入 array 的最尾端，並用 __swim() 實現了將節點往上浮 (swim) 的操作。
extract_max() 時，我們將最尾端的元素和最頂端的元素交換，並用 __sink() 實現了將節點往下沉 (sink) 的操作。

class MaxHeap:
	def __init__(self):
		self.heap = []

	def insert(self, item):
		self.heap.append(item)
		self.__swim(len(self.heap) - 1)

	def extract_max(self):
		value = self.heap[0]
		self.heap[0] = self.heap[-1]
		self.heap.pop()
		self.__sink(0)
		return value

	def __swim(self, k):
		while (k > 0 and self.heap[(k - 1) // 2] < self.heap[k]):
			self.__swap((k - 1) // 2, k)
			k = (k - 1) // 2

	def __sink(self, k):
		while (k * 2 + 1 < len(self.heap)):
			j = k * 2 + 1
			if (k * 2 + 2 < len(self.heap) and self.heap[k * 2 + 2] > self.heap[k * 2 + 1]):
				j = k * 2 + 2

			if (self.heap[j] > self.heap[k]):
				self.__swap(j, k)

			k = j

	def __swap(self, j, k):
		tmp = self.heap[j]
		self.heap[j] = self.heap[k]
		self.heap[k] = tmp